Evaluation of Lattice Boltzmann Method for transition flow simulation of Turbine Blades
Flow through gas turbine blades is a complex phenomenon as it should capture multiple phenomena such as separation, transition, relaminarization and effects of the high curvature of blade on the boundary layer. Traditional Reynolds Averaged Navier Stokes (RANS) based tools are inadequate to capture all these phenomena. SankhyaSutra Taral, based on Entropic Lattice Boltzmann Method (ELBM), can handle all these phenomena accurately.
LBM is becoming an increasingly popular alternative to traditional CFD methods owing to its simplicity and scalability on parallel computing architectures. The ELBM does not need explicit empirical modelling for small scales in under-resolved simulations, whose results are similar to Large Eddy Simulation (LES). The flow features are accurately resolved when a fine enough resolution is used giving Direct Numerical Simulation (DNS) level results. Thus, the use of ELBM ensures a seamless transition from LES to DNS by increasing the grid resolution.
The objective of this study is to assess and evaluate how ELBM can be used to understand the separated and transitional flows without the use of explicit turbulence models for low pressure turbine blades. Specifically, in this study we consider T106A (see Figure 1) and study the flow behavior for the incompressible regime.
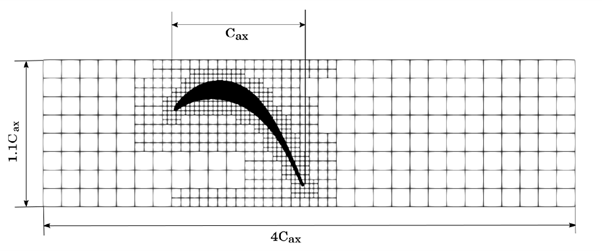
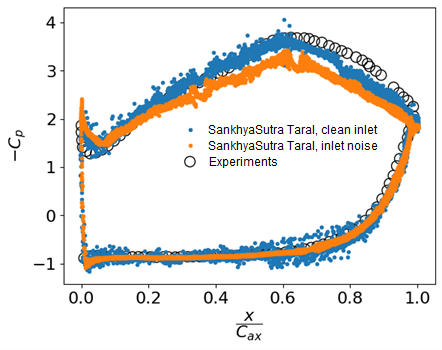
Two sets of simulations with 1024 and 1536 grid points per chord were carried out for the cases of clean inlet and inlet with disturbance. In Fig. 2, the time-averaged coefficient of pressure is shown on the blade surface. The reference pressure is the inlet pressure averaged over the pitch. As can be seen from the figures, Cp with clean inlet matches well with the experimental results, whereas the result with inlet disturbance overpredicts surface pressure near the trailing edge.
Inlet disturbance has no effect on the pressure side. In the turbulence-free inlet case, ideally the flow undergoes a natural transition from laminar to turbulent flow due to the instabilities arising at the separation bubble on the suction side. However, in the present case, we do not observe bypass transition, but the flow does become turbulent on the suction side.
To visualize the transition, we have plotted the y-component of velocity on the blade surface, along with the reference (Figure 3c) solution in which the velocity component is normal to the blade surface. Figure 3 clearly show the effect of inflow noise in tripping the flow to turbulence as inflow disturbances penetrate the boundary layer and trigger the separated shear layer.


Figure (3): The instantaneous velocity on the blade surface to visualise transition. (a) clean inlet, (b) with inlet disturbance and (c) velocity normal to surface (clean inlet)
As can be seen from these figures, for the clean inlet, the flow remains laminar throughout the blade surface and ordered Λ (Lambda) type vortices can be seen near the trailing edge. For the inlet case with noise, Λ structures form hairpin vortices downstream and further break down to form small scale structures. Although the flow structures near the blade surface are drastically different for the two cases, the pressure coefficient is similar as evidenced in Fig. 2. The comparisons given herein are for the qualitative flow structures, more detailed quantitative analysis of the flow field is in progress.
These results confirm that the pressure coefficient for T106A on the surface of the blade matches well with experimental results and establishes Entropic LBM as a promising method for simulation of transition flow.
Further reading: Hanumantharayappa et al, LES/DNS of flow past T106 LPT cascade using a higher-order LB model, AIAA Propulsion and Energy 2021 Forum.
