Scaling analysis of SankhyaSutra Taral

SankhyaSutra Taral is a state-of-the-art simulation platform for Computational Fluid Dynamics (CFD) based on the Entropic Lattice Boltzmann Method (LBM). A highly optimized parallel software implementation, SankhyaSutra Taral offers a model free approach for highly accurate CFD simulation. SankhyaSutra Taral provides a tremendous productivity boost to solve complex engineering problems and is designed to minimize dependence on long physical prototyping cycles. This document summarizes the scalability of SankhyaSutra Taral.

We consider a 3D simulation problem for scalability analysis. The computational domain is considered to have a fluid with uniform initial velocity magnitude of 1.571 x 10-3 m/s and kinematic viscosity of 1.571 x 10-5 m2/s. Periodic boundary condition is used in all directions. The flow evolves with time, which is recorded.

The analysis was done on SankhyaSutra Rudra cluster, which is an HPE Cray CS500 system with 256 nodes/ 32768 cores. Each node has an AMD EPYC 7742 processor with 2 x 64 physical cores, 512 GM of RAM and memory bandwidth of 410 Gbps.

We first performed weak scaling study. Here, the load on each Message Passing Interface (MPI) processor is kept the same and the number of processors is increased. This would result in an increase in total problem size as the number of processors increases. In other words, an increase in total process count by 2 would imply an increase in the domain length by 2 at the same grid resolution. Accordingly, domains with dimension [2m x 1m x 1m], [2m x 2m x 1m], [2m x 2m x 2m], [4m x 2m x2m], [4m x 4m x 2m], [4m x 4m x 4m] are used for simulation runs with 2, 4, 8, 16, 32 and 64 nodes, respectively, where each node has 128 cores. The domain is discretized uniformly in all three directions with a cell length of 3.90625 x 10-3 m.

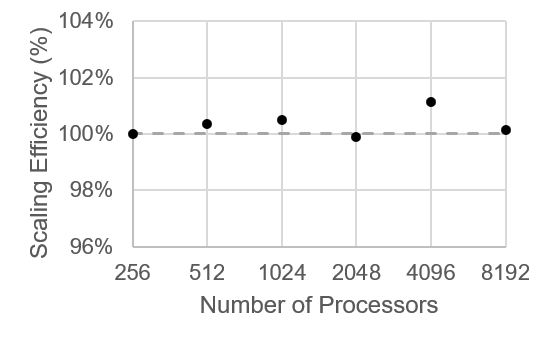
Figure 1: Weak scaling efficiency using 2 nodes with 256 MPI processes as reference

In weak scaling, the execution time per MPI process is expected to remain the same for all the configurations if the communication overhead is minimal compared to the memory access and computation per iteration. The time per iteration per MPI process for weak scaling study carried out using SankhyaSutra Taral is shown in Fig. 1. The variation in time by increasing the number of processors is almost negligible (<1.2%), indicating minimal communication overhead.

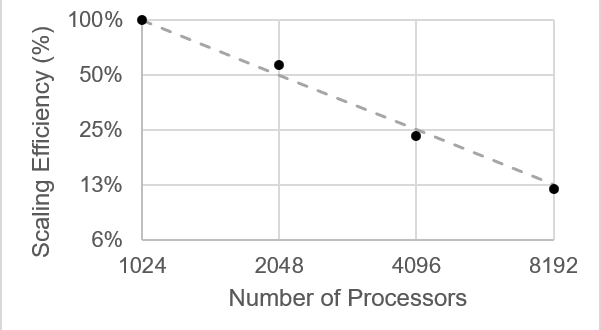
Next, we consider strong scaling analysis, where the system size is kept constant, and the compute resources are increased. This results in a decrease in problem size per processor as the number of processors increases. We present strong scaling analysis for a simulation setup with dimension of domain being [2m x 1m x 1m], which has 2048 x 1024 x 1024 grid points. Similar results are observed for domains with other dimensions.

For the chosen dimensions of the domain, the simulation system fits into the RAM for 8 nodes and ensures a balanced load distribution till 64 nodes, where each node has 128 cores. Figure 2 shows the strong scaling efficiency of SankhyaSutra Taral in comparison to the ideal case for a given system. The solver scales very well in the case of strong scaling.

Figure 2: Strong Scaling efficiency using 8 nodes with 1024 MPI processors as reference

It can be seen from Figures 1 and 2 that the SankhyaSutra Taral simulation software shows excellent weak and strong scaling for fluid flow simulations. This opens the possibility of running large-scale accurate simulations in a computationally efficient manner.

Download