Entropic Lattice Boltzmann Method for Stall Analysis

Due to high computational requirements of Direct Numerical Simulation (DNS), engineers and scientists use the Reynolds-averaged Navier-Stokes (RANS) method, where the mean flow is solved with an appropriate turbulence model for closure of Reynolds shear stress. RANS can provide reliable and accurate results for a variety of flows but fails to generalize to all flow conditions. For example, in the presence of large-scale unsteadiness in the mean flow, like the flow stalling over an airfoil or transitioning from laminar to turbulent flow regime, most of the turbulence models give erroneous results. The Lattice Boltzmann method is a mathematical formulation which can be used to overcome the technical limitations of RANS, while providing a high-fidelity solution with much lower memory requirements than DNS.

In this study, we look at stall analysis of an Eppler airfoil (E387) at a Reynolds number of 3 × 105 using SankhyaSutra Taral, which is based on higher-order entropic lattice Boltzmann method (ELBM). ELBM is developed to address the stability issues by adhering to the discrete H-theorem which is equivalent to the second law of thermodynamics in kinetic theory. SankhyaSutra Taral uses higher order LB model on a Body Centred Cubic (BCC) lattice.

The computational domain is 8.5𝑐 × 5𝑐 × 0.2𝑐, where c is the chord of the airfoil. Uniform velocity inlet and constant static pressure outlet boundary conditions are used in the simulation. In the lateral directions, top and bottom, free-slip boundary conditions are imposed. A Gaussian white noise is superimposed over the velocity at the inlet plane which causes the flow to transition from laminar to turbulent regime. The simulation is performed at a stall angle of 16° in accordance with the experimental data.

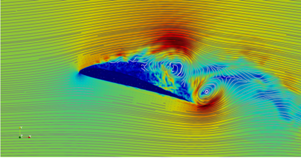
Fig. 1 Instantaneous velocity flow field at stall condition
Fig. 1 Instantaneous velocity flow field at stall condition

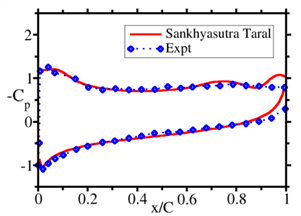
The qualitative flow field at angle of attack (AoA) of 160 is shown in Fig. 1. The flow separates at the leading edge causing the airfoil to stall. The separated rolls are seen in the instantaneous streamline plot. The coefficient of pressure for the simulation is shown in Fig. 2. On the pressure side of the blade, the coefficient of pressure matches quite well with the experiments. On the suction side there is a good match with the experiments while a discrepancy can be noted near the trailing edge for x/C greater than 0.85. The difference can be attributed to the low frequency oscillation in the flow at stall.

Fig. 2 Coefficient of pressure
Fig. 2 Coefficient of pressure
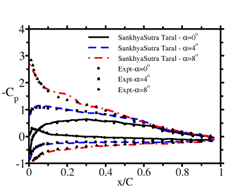
Fig. 3 Coefficient of pressure at pre-stall angle of attack
Fig. 3 Coefficient of pressure at pre-stall AoA

In order to understand the transition process from laminar to turbulent flow, the airfoil at pre-stall condition i.e. at AoAs of 0, 4 and 8 degrees, is simulated. The coefficient of pressure at the pre-stall angles of attack shows a good match with the experimental results as shown in Fig 3.

We have demonstrated the ability of the turbulence model-free ELBM to accurately predict separation and transition by simulating flow past the Eppler airfoil in pre-stall and stall regimes. The usual transition process typical of flow over airfoils in the Reynolds number range of 105 is well demonstrated. It is shown that at lower AoAs, the laminar boundary layer separates from the airfoil surface on the suction side, leading to a bubble, and re-attaches downstream. This separated shear layer undergoes a transition because of disturbances occurring in the laminar boundary layer. At higher AoAs, the separated boundary layer ceases to re-attach leading to a fully separated flow. All the simulations presented here do not use any explicit turbulence model to capture the flow dynamics.

Further reading: S. A. H. Rizvi, C. Thantanapally, S. Arcidiacono, and S. Ansumali. “Numerical simulation of separated flows using entropic lattice Boltzmann method”. AIAA Scitech 2023 Forum.

Download