Entropic Lattice Boltzmann Method for Cavity Aeroacoustics at Transonic Speeds

Understanding flow past open cavities and aerodynamic noise are crucial in many engineering applications. These flows have several applications such as designs of open sunroof, car window, landing gear wells, and weapon bay of an aircraft. Flow in open cavities results in self-sustaining oscillations, which can cause resonance leading to structural failure and undesirable sound. Therefore, an accurate understanding of cavity acoustics is essential to efficiently design cavities outside the flow excitation frequencies.

Lattice Boltzmann Method (LBM) is a promising method for handling acoustic problems due to its inherent ability to capture transient flow phenomena. From LBM simulations, in addition to accurate flow physics, acoustics data can be obtained by post-processing transient pressure signals. For simulating transonic flow over a cavity, we at SankhyaSutra Labs have used our in-house high-order Entropic Lattice Boltzmann Method (ELBM) solver on a Body-Centered Cubic (BCC) lattice.

Fig 1 Contours of instantaneous vorticity magnitude
In this work, the transonic flow in M219 cavity is simulated at a Mach number of 0.85 and Reynolds number of 6.7 × 106 based on the cavity length (0.508 m). The total pressure and temperature specified at the inlet are 100969 Pa and 309 K, respectively. The pressure data used for aeroacoustics analysis is recorded for 0.276 seconds with a sampling frequency of 307 kHz. This data is recorded after initial transients have settled. In the experiments, the pressure was recorded using 10 Kulite transducers placed equidistant on the centerline of the cavity roof. Figure 1 shows the contours of instantaneous vorticity magnitudes extracted at the cavity midsection in the YZ plane, with the x-axis representing the streamwise direction and the y-axis representing cross- stream direction. From the figure, we can observe intense vortex structures of broader scales throughout the length of the cavity. Figure 2 shows the root mean square pressure (Prms) along the cavity roof computed at the ten probe locations mentioned earlier. As can be seen from the figure, Prms match very well with experimental results.
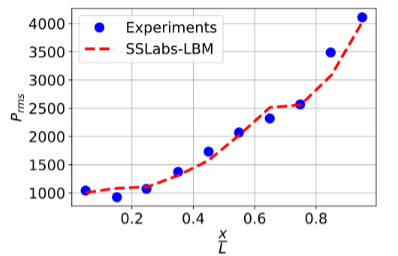
Fig 2: Root mean square pressure on the cavity roof at different pressure probe locations
Fig 2: Root mean square pressure on the cavity roof at different pressure probe locations

This case study demonstrates that the higher-order ELB method on the BCC lattice can accurately capture transonic aeroacoustic phenomena. We would like to highlight that the results presented do not use any explicit turbulence model; hence problem dependent ad-hoc tuning of turbulence model parameters is completely avoided.

For further details, see: Hanumantharayappa et al, A Model-Free Entropic Lattice Boltzmann Method for Cavity Aeroacoustics at Transonic Speeds, 28th AIAA/CEAS Aeroacoustics Conference, 2022

Download